臨床工学の分野の中でも,透析ってそれなりに数理的に遊んでみる余地のある分野かなと思います.物質移動や透析効率など,教科書にも数式のよく出てくる分野です.今回は,中空糸型ダイアライザの長手方向の圧力分布,流量分布について解析解を求めてみようと思います.
ダイアライザとは
腎臓の機能を代行する治療を一般に「透析」と呼び,その治療に必要な人工臓器をダイアライザと言います.ダイアライザにも幾つかの種類がありますが,現在臨床使用されているものの殆どは中空糸型と呼ばれるものです.今回はこの中空糸型ダイアライザ内の流れについてモデル化し,その理論解析を試みてみようと思います.下にその代表的な製品を挙げておきます.
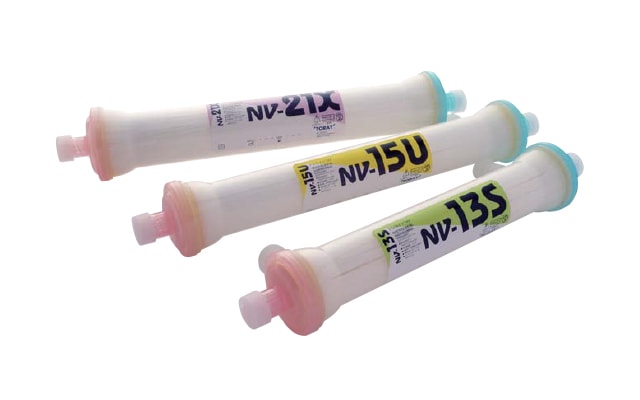
トレライトNV
東レ株式会社が製造販売しているポリスルホン膜の中空糸型ダイアライザ.(画像は東レのWEBサイトから引用)
中空糸型ダイアライザのモデル化
寸法パラメータを規定する
中空糸型ダイアライザの中身はどうなっているでしょうか.
右のカットイメージを見てもらえば分かるように,中空糸型ダイアライザの中身はパイプ状の透析膜が無数に束ねられた構造をしています.その両端は中空糸の開口部を残してポッティングされ膜の内側と外側が隔てられています.この寸法形状を規定するパラメータとしては,中空糸直径 ![]() ,中空糸有効長
,中空糸有効長 ![]() ,中空糸本数
,中空糸本数 ![]() ,有効膜面積
,有効膜面積 ![]() が挙げられ,その関係は次の通りです.
が挙げられ,その関係は次の通りです.
(1) ![]()
変数は4つありますが,陽に与えられるパラメータとしては ![]() を採用します.
を採用します.

流れる流体の量と圧のパラメータを規定する
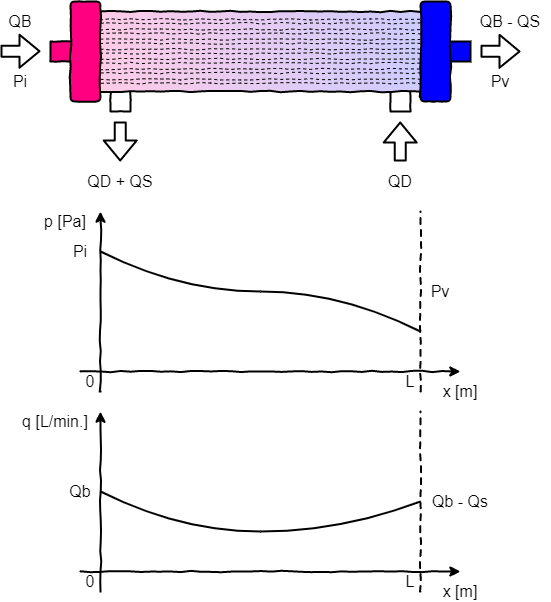
ダイアライザの模式図を右に示します.左の赤い部分が血液の入り口,青い部分が出口です.下に付いている2つの突起は透析液の出入り口を表していて,通常は透析液が血液と対向流となるように流します.
今回は中空糸の内側に流れる血液のダイアライザ長手方向に関する圧力分布と流量分布を求めることを目的としています.この分布をダイアライザの入口からの距離 ![]() を変数とした関数として表し,それぞれ圧力
を変数とした関数として表し,それぞれ圧力 ![]() と流量
と流量 ![]() とおきます.この分布はもちろん既に調べられていて,およそ右のグラフのようになると考えられています.しかし,具体的な関数系も含めて記述されているものは少ないのでこれを明らかにしていきます.
とおきます.この分布はもちろん既に調べられていて,およそ右のグラフのようになると考えられています.しかし,具体的な関数系も含めて記述されているものは少ないのでこれを明らかにしていきます.
各ポート出入り口における圧力と流量については,今後次の文字を使用します.
- 入口圧:
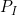
- 静脈圧(出口圧):
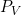
- 透析液圧:
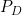
- 脱血流量:
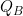
- 透析液流量:
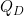
- 除水速度:
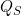
この時,関数 ![]() と
と ![]() の境界条件は次の通りになります.
の境界条件は次の通りになります.
(2) ![]()
中空糸内流れの関係式
中空糸の内側の流れを考えると,中空糸の内側と外側とでの交通はあるものの,局所的にはハーゲン・ポアズイユ流れを仮定できます.つまり,中空糸1本当たりの流量は圧力勾配と中空糸直径の4乗に比例すると考えられます.
(3) ![]()
式(1)を用いて ![]() を用いない形に変形したうえで比例定数を
を用いない形に変形したうえで比例定数を ![]() として次の式を立てることができます.
として次の式を立てることができます.
(4) ![]()
層間流れの関係式
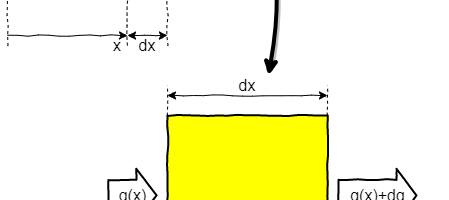
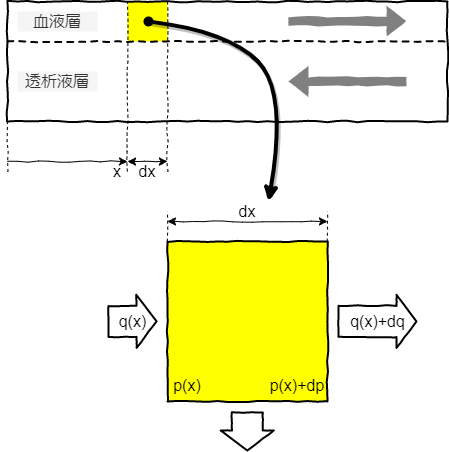
中空糸の内側から外側への流体の移動量について考えます.中空糸は円筒状のケースの中を半ば埋め尽くす程に多数固定され,血液と透析液はその内側と外側にそれぞれ接しています.ここではその構造を右の図に示すように簡略化し,血液層と透析液層がひとつの透析膜を介して接してると考えます.入口ポートからの距離が ![]() の微小な領域を切り出して流量のバランス(連続の式)を考えることで微分方程式を立式します.
の微小な領域を切り出して流量のバランス(連続の式)を考えることで微分方程式を立式します.
血液層での流量変化は血液層と透析液層との間の限外濾過によってもたらされると考え,その濾過流量は圧力較差と膜面積に比例すると仮定します.透析液層の圧力は全ての場所で一定の ![]() とし,血液層の圧力は
とし,血液層の圧力は ![]() で代表されるとすると,ダイアライザ全体の膜面積
で代表されるとすると,ダイアライザ全体の膜面積 ![]() と比例定数
と比例定数 ![]() を用いて次の関係が成り立ちます.ただし,浸透圧などは無視します.
を用いて次の関係が成り立ちます.ただし,浸透圧などは無視します.
(5) ![]()
微小量の積は無視し,整理すると次の式となります.
(6) ![]()
微分方程式を解く
解くべき連立微分方程式は先に立てた次の式です.
(7) 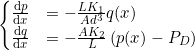
今回はちょっと手抜きします.
WolframAlpha で一般解を求める
ちょっとした式変形や,微分方程式を解いてもらったり,グラフを描いてもらうのに便利なサービスとして WolframAlpha が有名です.これでサクッと一般解を見つけてもらいましょう.解きたい式は独立変数を ![]() とした2つの関数
とした2つの関数 ![]() および
および ![]() についての連立一階微分方程式です.WolframAlpha で連立微分方程式を解かせる方法はちょっとググった感じでは無さげだったので,ひとつの二階微分方程式に書き直します.
についての連立一階微分方程式です.WolframAlpha で連立微分方程式を解かせる方法はちょっとググった感じでは無さげだったので,ひとつの二階微分方程式に書き直します.
(8) ![]()
これをこんな感じで解いてもらいます.定数係数は全て簡素化して入力しました.すると次のような結果が得られます.
DSolve[{p''[x] == a (-b + p[x])}, p[x], x]{p[x] == b + E^(Sqrt[a] x) Subscript[c, 1] + Subscript[c, 2]/E^(Sqrt[a] x)}定数係数を戻して分かりやすく書くと次のようになります.ただし,![]() および
および ![]() は積分定数で,
は積分定数で,![]() とおいて表記を簡潔にしています.
とおいて表記を簡潔にしています.
(9) ![]()
(10) ![]()
特殊解を求める
積分定数2つに対して境界条件を4つも用意しているので,そのうち2つを利用して特殊解を求めます.
圧力分布の境界条件を利用する場合
境界条件として ![]() を用いると,積分定数は次のようになり,特殊解が得られます.
を用いると,積分定数は次のようになり,特殊解が得られます.
(11) ![]()
(12) ![]()
(13) ![]()
(14) ![]()
ちなみに,このようにして WolframAlpha で一気に特殊解を得ることもできます.
DSolve[{p''[x] == a (-b + p[x]), p[0] == c, p[L] == d}, p[x], x]{p[x] == (b (-1 + E^(Sqrt[a] L)) (E^(Sqrt[a] L) - E^(Sqrt[a] x)) (-1 + E^(Sqrt[a] x)) + c (E^(2 Sqrt[a] L) - E^(2 Sqrt[a] x)) + d E^(Sqrt[a] L) (-1 + E^(2 Sqrt[a] x)))/(E^(Sqrt[a] x) (-1 + E^(2 Sqrt[a] L)))} (15) ![]()
一見異なる式に見えますが,式変形により同値であることが確認できます.
流量分布の境界条件を利用する場合
境界条件として ![]() を用いると,積分定数は次のようになり,特殊解が得られます.
を用いると,積分定数は次のようになり,特殊解が得られます.
(16) ![]()
(17) ![]()
(18) ![]()
(19) ![]()
![]() や
や ![]() に対して
に対して ![]() や
や ![]() は治療条件として陽に与えられるものなので,こちらの方法の方がより自然な表現となります.
は治療条件として陽に与えられるものなので,こちらの方法の方がより自然な表現となります.
圧力境界条件解と流量境界条件解の関係性
圧力分布の境界条件を利用した場合でも,流量分布の境界条件を利用した場合でも,それにより求まる積分定数 ![]() は式 (11)と式 (16),式 (12)と式 (17) でそれぞれ同じ値となるはずです.
は式 (11)と式 (16),式 (12)と式 (17) でそれぞれ同じ値となるはずです.
(20) ![]()
(21) ![]()
この2式を整理すると次の2式となります.
(22) ![]()
(23) ![]()
![]() はダイアライザの材料定数として,
はダイアライザの材料定数として,![]() は治療条件として,
は治療条件として,![]() は運転条件として given なパラメータであると考えるとそれらによって
は運転条件として given なパラメータであると考えるとそれらによって![]() が計算可能であることが分かります.
が計算可能であることが分かります.
陽に与えられるパラメータのみで表現する
式(23)を利用して式(18)を given なパラメータのみで表すと次のようになります. ただし,![]() としています.
としています.
(24) ![]()
また,式(19)も ![]() の代わりに
の代わりに ![]() を用いると次のようになります.
を用いると次のようになります.
(25) ![]()
除水なしの場合
除水なし,すなわち ![]() の場合は次のようになります.
の場合は次のようになります.
(26) ![]()
(27) ![]()
長くなってきたので,今回はここまで!