VV ECMO における再循環率の推定方法を再考する

COVID-19 関連のニュースにも登場するようになった ECMO（ VV ECMO ）ですが，VV ECMO の再循環率の計算式って実際には使いづらいですよね．それ実測できないしどこで代用する？って話しにいつもなると思います．確実に測定できる項目だけを使って計算できないのか，考えてみました．

ECMOとは

膜型人工肺を用いた体外循環による心肺補助法のことを英語で extracorporeal membrane oxygenation といい，その略称であるECMOが日本でも一般的に使用されています．具体的には，脱血カニューレから血液を体外に導き，遠心ポンプと熱交換器付き人工肺を通して送血カニューレから体内に戻します．流れの駆動力は遠心ポンプから得られる揚程により生み出され，熱交換器で血液温度を調整し，人工肺では酸素濃度が適切に調整されたスイープガスにより還元ヘモグロビンの酸素化と溶存二酸化炭素の除去が行われます．数日から数週間に渡り心肺機能を代行する究極の対症療法であり，心原性ショックや可逆性重症呼吸不全に対する切札となり得るものです．

これに似たものとして遠心ポンプを用いた体外式左室補助人工心臓（体外式 LVAD）と呼ばれるものもありますが，こちらは左心機能を代行することを目的としているため人工肺が必須の要素とはなりません．人工肺が付いている場合には LVAD ではなく，敢えて LVAD-ECMO と呼ぶこともあります．

ECMOの分類

ECMO にも治療戦略に合わせて様々なバリエーションがあり，治療目的や送脱血部位によりある程度の呼び分けがされています．補助対象により分類すると，循環補助を主目的とした cardiac ECMO と，呼吸補助を主目的とした respiratory ECMO の2つに大別されます．特定の目的に対する呼称もあり，ECMO を利用した心肺蘇生法の名称である ECPR，体外循環を用いた二酸化炭素除去方法である ECCO2R と呼ばれるものもあります．

cardiac ECMO
respiratory ECMO
ECPR（ extracorporeal cardiopulmonary resuscitation ）
ECCO2R（ extracorporeal CO2 Removal ）

また，血管系へのアクセス部位が心臓に近いか遠いかで次の2種類に分けることが出来ます．

central ECMO
peripheral ECMO

さらに，カニュレーション部位が動脈なのか静脈なのかにより次の2種類に分類できます．

VA ECMO（ veno-arterial extracorporeal membrane oxygenation ）
VV ECMO（ veno-venous extracorporeal membrane oxygenation ）

静脈脱血と動脈送血を行うものを VA ECMO と呼び，静脈脱血と静脈送血を行うものを VV ECMO と呼びます．またこれらの組み合わせとして，静脈から脱血し動脈と静脈の双方に送血する VVA ECMO 又は VAV ECMO と呼ばれる形式のものもあります．

これらの分類はそれぞれ何によって分類するかの違いであり，文脈により色々な組み合わせで使われます．例えばVF・CPAに対してECPR を行う場合，補助目的は cardiac ECMO となり，その構成は peripheral VA ECMO となります．日本においてはこの peripheral VA ECMO のことを PCPS（ percutaneous caidiopulmonary support ）と呼ぶことが多いです．また，ARDS に対して respiratory ECMO を導入する場合，その構成は peripheral VV ECMO となりますが，central VV ECMO となることはまずないので普通これは VV ECMO と呼びます．

VV ECMO

VV ECMO は基本的に Peripheral ECMO であり，Respiratory ECMO を実現する手段となります．送脱血ポイントは共に大静脈内もしくは右心房（ RA : right atrium ）にあり，VA ECMO と比較して直接的には循環動態に影響を及ぼしません．

送脱血カニューレの留置位置には幾つかのバリエーションがあります．大腿静脈（ FV : femoral vein ）から挿入した脱血カニューレ先端を下大静脈（ IVC : inferior vena cava ）内に留置し，右内頸静脈（ Rt. JV : right internal jugular vein ）から挿入した送血カニューレ先端を RA に留置する方法が一般的です．もしくは，FV から挿入した脱血カニューレ先端を IVC に留置し，対側の FV から挿入した送血カニューレ先端を RA に留置する方法もあります．更に AVALON ELITE Bi-Caval Dual Lumen Catheter のようなダブルルーメンカテーテルが使える場合には，これを Rt. JV から挿入する方法もあります．

シングルルーメンカテーテルを2本使用する場合
- 【脱血】FVアプローチ・先端IVC　【送血】FVアプローチ・先端RA
- 【脱血】FVアプローチ・先端IVC　【送血】Rt.JVアプローチ・先端RA
ダブルルーメンカテーテルを1本使用する場合
- Rt.JVアプローチ・送血点RA・脱血点SVC＋IVC

VV ECMO を確立させる上で問題になるポイント

VV ECMO は VA ECMO と異なり同じ血管内の比較的近い場所に送脱血カニューレの先端が位置するため，特有の問題が起こってきます．どれだけうまくカニュレーションが行われたとしても，静脈還流血を全て余すことなく脱血し，酸素化された血液を全て逃さず右心系へと送り込むことはできないということです．例えば，送脱血カニューレの先端が近すぎる場合には同じ血液が ECMO 回路内を巡回し続けることで，実質的な呼吸補助の程度が著しく低下してしまいます．その為，送脱血カニューレを適切な位置に留置することが VV ECMO を確立させる上では重要となり，更には補助の程度を定量的に把握する手段を持つ必要があります．

先に述べた「同じ血液が ECMO 回路内を巡回し続ける」現象のことを再循環（リサーキュレーション）と呼びます．この程度を表す指標として，再循環率（リサーキュレーション率）と呼ばれるものがあり，定義としては「ECMO システムから送血された血液が肺動脈へと流れず再び ECMO システムへ脱血される割合」となります．

これを推定する方法について今回は考えてみます．

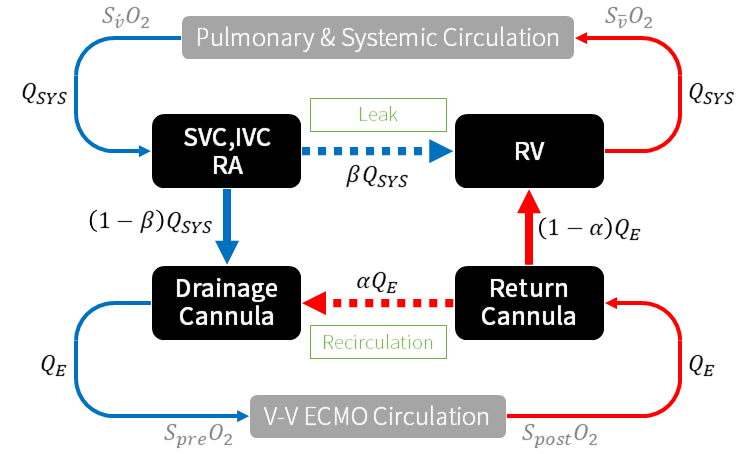
再循環を考慮した VV ECMO の血液循環モデル

再循環を考慮に入れた VV ECMO の血液循環経路を次の図に示します．図中の上半分の経路が VV ECMO を含まない全身の血液循環を，下半分が VV ECMO の血液循環を表し，それぞれの灌流量を $Q_{\mathrm{SYS}} \, \mathrm{[L/min.]}$ ， $Q_{\mathrm{E}} \, \mathrm{[L/min.]}$ とおきます．全身灌流の終点と起点をそれぞれ [SVC,IVC,RA] と [RV] と考え，その終点に ECMO の脱血カニューレが接続されていて，その起点に送血カニューレが接続されていると考えます．[Recirculation] は送血カニューレから脱血カニューレに流れる経路として表現し，再循環の相補的な現象である ECMO を通らずに（ ECMO の脱血からリークして）全身循環へ戻る血流は [Leak] として表現しています．

再循環を起こさず理想的な血液循環となっている場合には，血液は図中の実線で記された経路を流れることとなり VV ECMO が全身循環に直列的に挿入される状態となりますが，完全な再循環を引き起こしている場合には上下の経路がそれぞれ独立の経路となり VV ECMO の効果が全くない状態となります．

ここで，再循環率を $\alpha$ ，還流した静脈血がリークする割合であるリーク率を $\beta$ とおくと，VV ECMO の脱血量に着目して次の関係が成り立ちます．

(1) $\begin{equation*} \alpha Q_{\mathrm{E}} + (1-\beta) Q_{\mathrm{SYS}} = Q_{\mathrm{E}} \end{equation*}$

式変形により $\beta$ を $\alpha$ を用いて表すと次のようになります．

(2) $\begin{equation*} \beta = 1- \frac{Q_{\mathrm{E}}}{Q_{\mathrm{SYS}}}(1-\alpha)\end{equation*}$

ここから， $\alpha$ と $\beta$ は従属変数の関係にあり，どちらかのみに着目していれば良いことが分かります．一般に話題にされるパラメータが再循環率だけで，リーク率が取り上げられない慣習は妥当だと言えるでしょう．両者とも本質的に同じ現象であり，見方を変えたパラメータということになります．実際， $Q_{\mathrm{E}}$ は当然装置の流量計から読み取れ， $Q_{\mathrm{SYS}}$ は心拍出量として肺動脈カテーテルなどにより測定可能である場合が殆どであり，一方が分かれば他方は簡単に算出出来ます．

次に，ヘモグロビンに結合した酸素の移動量について考えます．血流による結合酸素移動量は，血液流量とヘモグロビン濃度及びヘモグロビンの酸素結合係数及び酸素飽和度の積によって表せます．しかし，ヘモグロビン濃度及びヘモグロビンの酸素結合係数は血液循環経路のすべての場所で一定とみなせるため，回路内の酸素移動量は血液流量と酸素飽和度の積により比較可能となります．ここで，還流した静脈血の酸素飽和度を仮想的混合静脈血酸素飽和度 $S_{\acute{\mathrm{v}}}O_2$ ，肺動脈にて測定される混合静脈血酸素飽和度を $S_{\overline{\mathrm{v}}}O_2$ ，V-V ECMO 脱血側の酸素飽和度を人工肺前血酸素飽和度 $S_{\mathrm{pre}}O_2$ ，V-V ECMO 送血側の酸素飽和度を人工肺後血酸素飽和度 $S_{\mathrm{post}}O_2$ とおくと，VV ECMO に取り込まれる酸素の量と，全身に送られる酸素の量に関して次の2つの式が成り立ちます．

(3) $\begin{equation*}(1-\beta) Q_{\mathrm{SYS}} S_{\acute{\mathrm{v}}}O_2 + \alpha Q_{\mathrm{E}} S_{\mathrm{post}}O_2 = Q_{\mathrm{E}} S_{\mathrm{pre}}O_2\end{equation*}$

(4) $\begin{equation*}\beta Q_{\mathrm{SYS}} S_{\acute{\mathrm{v}}}O_2 + (1-\alpha) Q_{\mathrm{E}} S_{\mathrm{post}}O_2 = Q_{\mathrm{SYS}} S_{\overline{\mathrm{v}}}O_2\end{equation*}$

この両式に式(2)を代入すると次の2つの式になります．

(5) $\begin{equation*} Q_{\mathrm{E}} (1-\alpha) S_{\acute{\mathrm{v}}}O_2 + \alpha Q_{\mathrm{E}} S_{\mathrm{post}}O_2 = Q_{\mathrm{E}} S_{\mathrm{pre}}O_2\end{equation*}$

(6) $\begin{equation*} \left\{ Q_{\mathrm{SYS}} - Q_{\mathrm{E}} (1-\alpha) \right\} S_{\acute{\mathrm{v}}}O_2 + (1-\alpha) Q_{\mathrm{E}} S_{\mathrm{post}}O_2 = Q_{\mathrm{SYS}} S_{\overline{\mathrm{v}}}O_2\end{equation*}$

式(5)を変形すると次の式となり，これは一般的によく知られた VV ECMO の再循環率を求める式と一致しています．

(7) $\begin{equation*} \alpha = \frac{S_{\acute{\mathrm{v}}}O_2 - S_{\mathrm{pre}}O_2}{S_{\acute{\mathrm{v}}}O_2 - S_{\mathrm{post}}O_2} = \frac{S_{\mathrm{pre}}O_2 - S_{\acute{\mathrm{v}}}O_2}{S_{\mathrm{post}}O_2 - S_{\acute{\mathrm{v}}}O_2}\end{equation*}$

Identification and management of recirculation in venovenous ECMO
https://www.elso.org/Portals/0/Files/ELSO_Recirculation_guideline_May2015.pdf

式は求まりました．しかし，ここで問題がひとつ出てきます． $S_{\acute{\mathrm{v}}}O_2$ が実測できないということです．VV ECMO の送血に影響を受けず，上半身からの静脈還流と下半身からの静脈還流が混合した状態での酸素飽和度が測れるでしょうか．無理ですね．実際にはここで妥協して，中心静脈カテーテルから採血した静脈血の酸素飽和度で代用したりしますが，あまり納得できるサロゲートではありませんね．

混合静脈血酸素飽和度で表現する方法

$S_{\acute{\mathrm{v}}}O_2$ を実測することは困難ですが， $S_{\overline{\mathrm{v}}}O_2$ は Swan-Ganz カテーテルにより簡単に実測が可能です．そこで，関係式(6)を利用し， $S_{\acute{\mathrm{v}}}O_2$ を含まない式により再循環率を表す方法を取ってみます．式(6)に式(7)を代入して整理すると次の関係式が得られます．

(8) $\begin{equation*}S_{\acute{\mathrm{v}}}O_2 = S_{\overline{\mathrm{v}}}O_2 - \frac{Q_{\mathrm{E}}}{Q_{\mathrm{SYS}}} \left( S_{\mathrm{post}}O_2 - S_{\mathrm{pre}}O_2 \right)\end{equation*}$

これを式（7）に代入することで， $S_{\acute{\mathrm{v}}}O_2$ を含まない形で再循環率を表せます．

(9) $\begin{equation*}\alpha = \frac{Q_{\mathrm{SYS}} \left( S_{\mathrm{pre}}O_2 - S_{\overline{\mathrm{v}}}O_2 \right) + Q_{\mathrm{E}} \left( S_{\mathrm{post}}O_2 - S_{\mathrm{pre}}O_2 \right)}{Q_{\mathrm{SYS}} \left( S_{\mathrm{post}}O_2 - S_{\overline{\mathrm{v}}}O_2 \right)+ Q_{\mathrm{E}} \left( S_{\mathrm{post}}O_2 - S_{\mathrm{pre}}O_2 \right)}\end{equation*}$

VV ECMO の流量と心拍出量との比を $\gamma$ とすると次の形になります．

(10) $\begin{equation*}\alpha = \frac{S_{\mathrm{pre}}O_2 - S_{\overline{\mathrm{v}}}O_2 + \gamma \left( S_{\mathrm{post}}O_2 - S_{\mathrm{pre}}O_2 \right)}{S_{\mathrm{post}}O_2 - S_{\overline{\mathrm{v}}}O_2 + \gamma \left( S_{\mathrm{post}}O_2 - S_{\mathrm{pre}}O_2 \right)}\end{equation*}$

人工肺出口の血液の酸素飽和度は，人工肺の劣化が考えられる状況や定格外使用をしていない限り，ほぼ100％であることが殆どであるため， $S_{\mathrm{post}}O_2 = 1$ とすると更に簡略化できます．

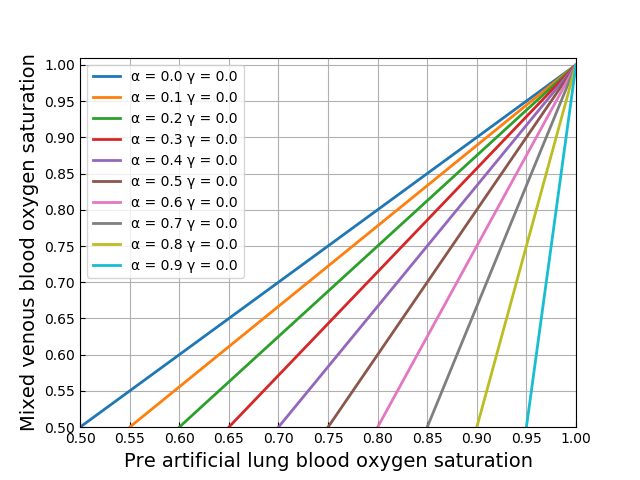
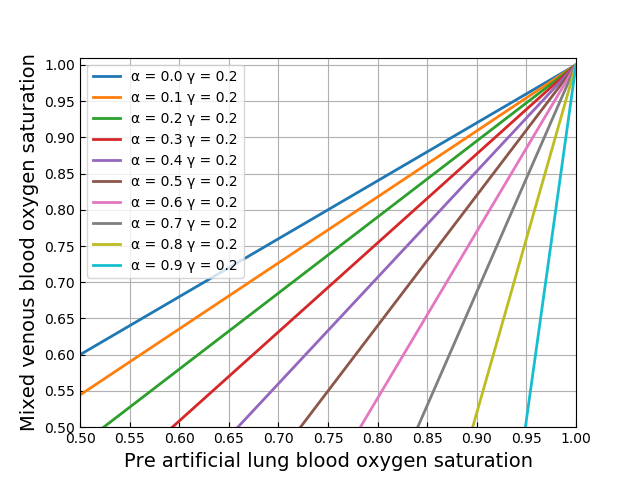
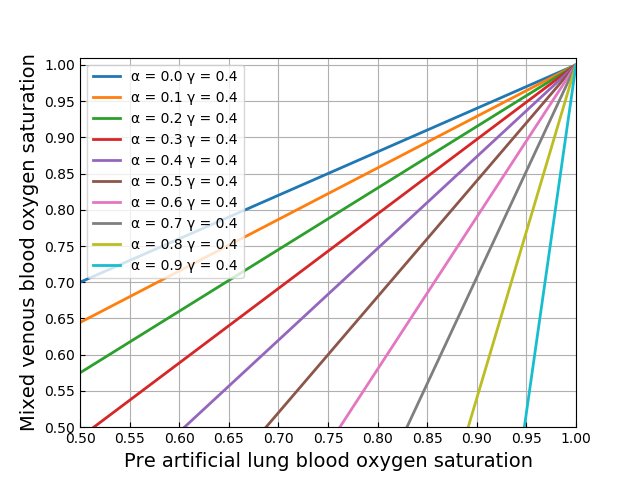
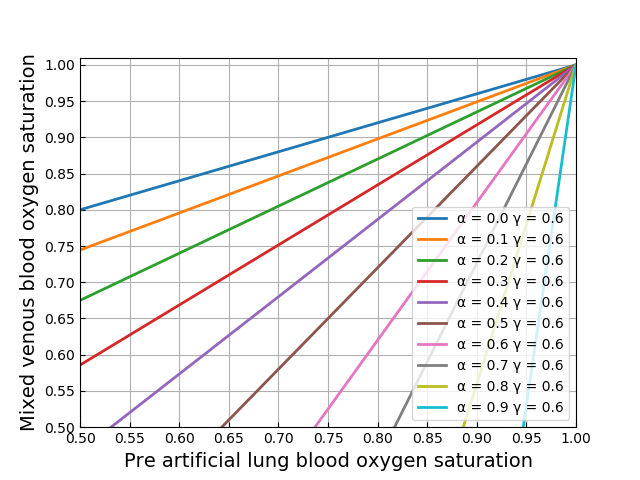
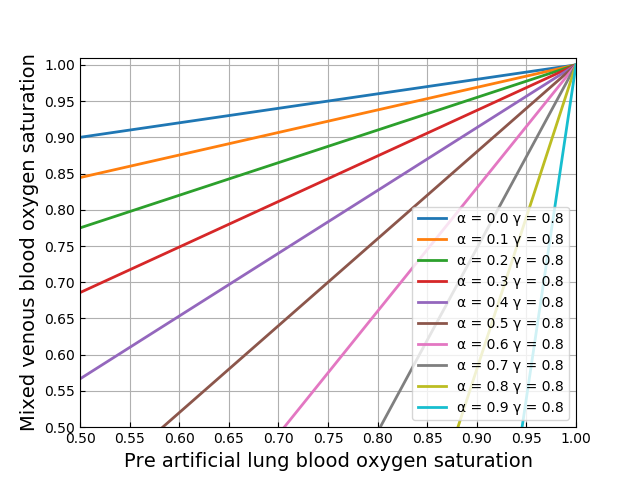
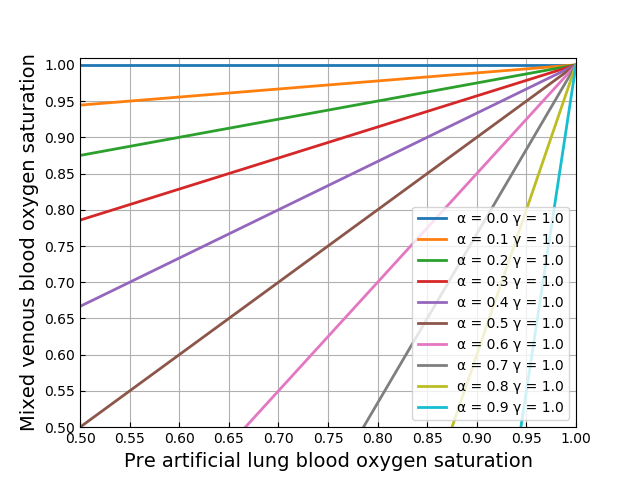
(11) $\begin{equation*} \alpha = \frac{S_{\mathrm{pre}}O_2 - S_{\overline{\mathrm{v}}}O_2 + \gamma \left( 1 - S_{\mathrm{pre}}O_2 \right)}{1 - S_{\overline{\mathrm{v}}}O_2 + \gamma \left( 1 - S_{\mathrm{pre}}O_2 \right)}\end{equation*}$

グラフ化

横軸に $S_{\mathrm{pre}}O_2$ 縦軸に $S_{\overline{\mathrm{v}}}O_2$ を取った平面上に再循環率を図示することを考えてみます．式(11)を次のように変形すると， $S_{\overline{\mathrm{v}}}O_2$ が $S_{\mathrm{pre}}O_2$ に関する1次関数の形で表せます．

(12) $\begin{equation*}S_{\overline{\mathrm{v}}}O_2 = \frac{\alpha\gamma -\gamma +1}{1-\alpha}S_{\mathrm{pre}}O_2 + \frac{-\alpha\gamma -\alpha +\gamma}{1-\alpha}\end{equation*}$